Czym jest metoda gradientu prostego (gradient descent)?

Gradient descent to jedna z podstawowych technik stosowanych w uczeniu maszynowym i sztucznej inteligencji. Pozwala modelom stopniowo poprawiać parametry tak, aby ich przewidywania stawały się coraz trafniejsze.

Trening modelu można opisać dość prosto, nawet jeśli w tle działa złożona matematyka. Podajemy pytanie z poprawną odpowiedzią, model odpowiada na podstawie losowo ustawionych parametrów, a następnie porównujemy wynik z wartością oczekiwaną. Różnica między nimi pokazuje, jak bardzo model się pomylił. Na tej podstawie korygujemy parametry tak, aby kolejna próba była choć trochę lepsza. Cały proces powtarza się wiele razy, aż model zacznie rozpoznawać wzorce.

Tak działa gradient descent: wskazuje kierunek zmiany parametrów oraz siłę tej zmiany, co porównuje się do schodzenia w kierunku najniższego punktu doliny. Ponieważ problemy są zbyt złożone, aby wyliczyć parametry dokładnie, metoda korzysta z przybliżeń i stopniowego zbliżania się do najlepszego rozwiązania.

Dzięki temu działa większość współczesnych modeli, od sieci neuronowych po techniki regresyjne, które analizują tekst, liczby i obrazy. Bez gradient descent rozwój dzisiejszej AI byłby praktycznie niemożliwy.

Gradient descent, czyli schodzenie po zboczu.

Najłatwiej ująć to obrazowo. Załóżmy, że stoisz na szczycie góry w ciemności. Nie widzisz otoczenia, ale możesz wyczuć, w którą stronę teren opada. Każdy krok w dół przybliża cię do doliny, czyli miejsca, w którym błąd modelu jest najmniejszy. Gradient descent działa podobnie: wykorzystuje lokalną informację o nachyleniu powierzchni, żeby określić kierunek ruchu.

Ta intuicja sprawia, że metoda działa nawet wtedy, gdy funkcja kosztu jest skomplikowana i ma wiele wymiarów. Model nie musi znać całego krajobrazu matematycznego, wystarczy mu informacja o lokalnym nachyleniu.

Analogia do schodzenia po zboczu jest bardzo ciekawa, ale jak to przełożyć na liczby, które potem generują tekst, obrazy, czy wykonują analizy?

Trenowanie modeli AI można sprowadzić do prostej sytuacji: mamy wzór, na przykład$$\hat{y} = a x + b,$$

i chcemy, aby dla danego $x$x dawał wynik jak najbardziej zbliżony do prawdziwego $y$. Problem polega na tym, że nie znamy dobrych wartości $a$ i $b$. Na początku ustawiamy je losowo, na przykład $a = 0$ i $b = 0$. Jeśli podstawimy $x = 2$x=2, model przewidzi$$\hat{y} = 0 \cdot 2 + 0 = 0,$$

ale załóżmy, że prawidłowa odpowiedź to $y = 5$. Różnica między 0 a 5 to błąd, który informuje nas, jak bardzo model się myli.

Na podstawie tej różnicy decydujemy, jak zmodyfikować parametry. Jeśli wynik był za mały, należy zwiększyć $a$ i $b$. Jeśli za duży, trzeba je zmniejszyć. Nie wyliczamy idealnych wartości, bo problem jest zbyt złożony, nawet w większych modelach z milionami parametrów. Zamiast tego robimy przybliżenia: poprawiamy parametry o niewielką część błędu i sprawdzamy efekt. Powtarzamy to wiele razy, aż model zacznie trafiać coraz bliżej prawdy.

Właśnie tu pasuje analogia do schodzenia po zboczu. Kierunek zejścia mówi nam, które parametry trzeba zmienić: czy $a$a powinno rosnąć, czy maleć; czy $b$b trzeba podnieść czy obniżyć. „Stromość” zbocza to z kolei informacja, jak bardzo powinniśmy je zmienić: mały wpływ błędu oznacza delikatną korektę, duży wpływ wymaga mocniejszej zmiany.

Model nie widzi całego terenu, nie zna idealnych wartości, ale dzięki tym lokalnym wskazówkom, kierunkowi i wielkości zmian, potrafi stopniowo zbliżać się do rozwiązania, w którym błąd jest możliwie najmniejszy.

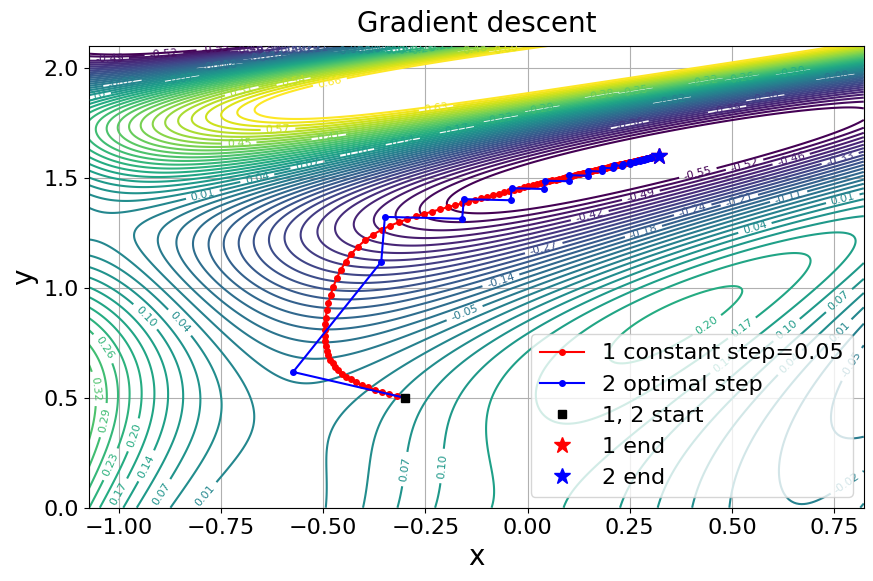
Co dzieje się podczas jednego kroku gradient descent

Proces uczenia rozpoczyna się od funkcji kosztu. Funkcja ta określa, jak duży jest błąd modelu. Na przykład w regresji liniowej często używa się błędu średniokwadratowego, czyli średniej różnicy między przewidywaniami a rzeczywistymi wartościami.

Gradient jako kierunek ruchu

Gradient to zestaw pochodnych, które wskazują kierunek najszybszego wzrostu funkcji kosztu. Ponieważ chcemy zmniejszać błąd, poruszamy się w przeciwną stronę. To właśnie gradient określa, w jaką stronę wagi modelu powinny zostać przesunięte, żeby funkcja kosztu była mniejsza.

Przy tym warto wiedzieć, że gradient może być różnej wielkości. Duży gradient oznacza strome zbocze i prowadzi do większych korekt. Mały gradient sygnalizuje płaską powierzchnię i powoduje tylko delikatne zmiany parametrów.

Aktualizacja wag modelu

Podstawowa formuła aktualizacji wag wygląda tak:
nowa waga = stara waga minus współczynnik uczenia pomnożony przez gradient.

To prosta zasada, ale jej powtarzanie w tysiącach lub milionach iteracji prowadzi do stopniowego zmniejszenia błędu i zbliżenia modelu do optymalnych parametrów.

Po każdej zmianie oblicza się nowy błąd i wykonuje kolejny krok. Proces trwa dopóki model się stabilizuje albo dopóki spełni określone kryteria zatrzymania, na przykład minimalną zmianę błędu.

Gradient Descent a backpropagacja

Gradient descent i backpropagacja to dwa elementy jednego procesu. Pierwszy odpowiada za to, w którą stronę przesunąć parametry, a drugi za to, jak policzyć ten kierunek dla każdego parametru w całej sieci. Razem tworzą mechanizm, który pozwala trenować modele o wielu warstwach, bez potrzeby ręcznego liczenia tysięcy pochodnych.

Można to ująć w kilku krokach. Najpierw gradient descent potrzebuje informacji o tym, jak zmienia się błąd wraz z parametrami. Sama metoda mówi jedynie, że musimy iść w kierunku przeciwnym do gradientu, aby zmniejszać błąd. Nie mówi natomiast, jak policzyć gradient sieci, która ma setki warstw, nieliniowe funkcje aktywacji i miliony wag. Tutaj wchodzi backpropagacja, która oblicza potrzebne pochodne w sposób uporządkowany (od wyjścia sieci w stronę wejścia), wykorzystując regułę łańcuchową i zapisując wyniki pośrednie, aby nie liczyć niczego powtórnie.

W praktyce wygląda to tak, że po wykonaniu jednego przejścia sieci do przodu otrzymujesz wynik oraz błąd. Następnie backpropagacja rozkłada ten błąd na mniejsze fragmenty, przypisując jego część każdej wadze i każdemu neuronowi. Na końcu masz pełną informację o tym, jak każda pojedyncza zmiana parametru wpłynęłaby na błąd. Gradient descent wykorzystuje te dane i aktualizuje wagi o niewielką wartość zależną od tempa uczenia.

W ten sposób backpropagacja dostarcza gradientu, a gradient descent wykonuje krok aktualizacji. Oba elementy działają więc razem, tworząc zamknięty cykl: przód sieci, obliczenie błędu, backpropagacja, aktualizacja parametrów, ponowne przejście przodu. Iteracje tego cyklu pozwalają zbliżać się do rozwiązania, którego nie da się zapisać w postaci jednego równania.

Gradient Descent na prostym przykładzie liczbowym.

Wróćmy do naszego prostego przykładu, ale tym razem rozważymy go dokładniej. $$\hat{y} = w x + b$$

i chcemy , żeby ten wzór dawał wynik jak najbardziej zbliżony do prawdziwej wartości $y$. Problem polega na tym, że nie znamy dobrych wartości zmiennych $w$ oraz $b$. Mamy tylko dane wejściowe $x$ i znane wyniki $y$. Twoim zadaniem jest nauczyć wzór odpowiednich wartości parametrów.

Gradient descent robi to w trzech prostych krokach, które powtarza wiele razy.

Krok 1: obliczamy wynik wzoru

Najpierw podstawiamy aktualne wartości zmiennych. Na początku zwykle są losowe lub zerowe.
Jeśli $w = 0$ i $b = 0$, to przewidywanie modelu dla dowolnego $x$ wynosi$$\hat{y} = 0 \cdot x + 0 = 0$$

Krok 2: obliczamy błąd

Ponieważ znamy prawdziwy wynik $y$, możemy policzyć, jak bardzo się pomyliliśmy.
Przykład: prawdziwy wynik to $y = 5$y=5, model przewidział $0$. Błąd to różnica

$$\hat{y} – y = 0 – 5 = -5$$

Możesz traktować to jako informację zwrotną: model mówi, co wyszło z jego wzoru, a my porównujemy to z prawdą.

Krok 3: poprawiamy zmienne na podstawie błędu

Tutaj zaczyna się istota gradient descent.
Jeśli model przewiduje zbyt mało, aktualizujemy zmienne tak, aby w następnym kroku przewidywania były większe. Jeśli przewiduje za dużo, zmienne zmieniamy w przeciwnym kierunku.

W praktyce stosujemy prostą regułę:

$$\text{nowa wartość} = \text{stara wartość} – \alpha \times \text{wpływ błędu}$$

gdzie $\alpha$ to tempo uczenia, czyli to, jak duży krok chcemy zrobić. Tempo uczenia to po prostu liczba którą co do zasady wybiera się ręcznie. Zbyt małe tempo uczenia powoduje że trenowanie jest bardzo wolne za to progres jest zauważalny przy każdej iteracji, zbyt duże tempo uczenia powoduje że model może „skakać” wokół wyniku, i nigdy „nie zejdzie na dół”.

Są również techniki pozwalające automatycznie dostosować tempo uczenia do określonych potrzeb, czyli optymalizatory adaptacyjne, np. Adam, RMSProp czy Adagrad. One modyfikują efektywne tempo uczenia w trakcie treningu, dostosowując je do zachowania gradientów. Jednak nawet przy tych metodach również musimy wybrać wartość początkową.

O jakich liczbach mówimy?

0.1 – duże tempo uczenia, używane raczej w prostych modelach albo na wczesnym etapie uczenia;

0.01 – bardzo popularna wartość w klasycznych metodach i wielu optymalizatorach;

0.001 – najczęstszy wybór w nowoczesnych modelach, zwłaszcza sieciach neuronowych;

0.0001 i mniej – stosowane, gdy model jest bardzo czuły albo gradienty są niestabilne.

To, co tu nazywam „wpływem błędu”, to właśnie gradient, Gradient to po prostu informacja: jak bardzo dana zmienna przyczyniła się do błędu. Jeśli wpływ jest duży, zmieniamy ją bardziej. Jeśli mały, zmiana jest subtelna.

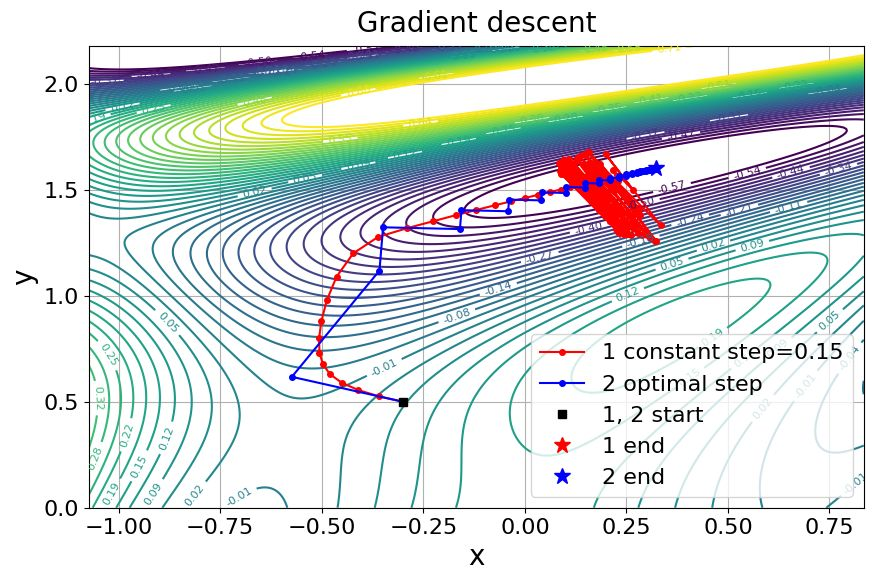
Dlaczego to działa

Za każdym razem poprawiamy zmienne na podstawie tego, co model zrobił źle. Jeśli błąd jest duży, zmienne korygują się mocniej; jeśli maleje, zmiany stają się mniejsze. Po wielu powtórzeniach wartości parametrów zaczynają „pasować” do danych, a przewidywania stają się coraz dokładniejsze.

Można to porównać nie do schodzenia po zboczu, lecz do zgadywania:

1. Zgadujemy wartości zmiennych.
2. Sprawdzamy, jak bardzo się pomyliliśmy.
3. Na podstawie błędu poprawiamy zgadywane wartości.
4. Powtarzamy aż zgadywanie stanie się bardzo dobre.

Gradient descent to po prostu systematyczne poprawianie zgadywanych wartości zmiennych, aż wzór przestanie się mylić.

Typowe problemy w pracy z gradient descent

Choć metoda jest uniwersalna i prosta, w praktyce pojawiają się trudności.

Lokalne minima i płaskie powierzchnie

Funkcja kosztu dla rzeczywistych modeli nie jest gładką miską, lecz czymś przypominającym skomplikowany krajobraz. Zdarza się, że model zatrzyma się w miejscu, które jest dobre, ale nie najlepsze. Lokalnych minimów można uniknąć, stosując losowe mieszanie danych, odpowiednie warianty uczenia lub dodatkowe mechanizmy.

Płaskie obszary powodują, że gradient jest bardzo mały i model wykonuje minimalne kroki. To naturalne zjawisko w dużych sieciach neuronowych, które potrafią mieć obszary, gdzie pochodne są bliskie zera.

Niestabilność i oscylacje

Jeśli learning rate jest zbyt wysoki, model może wykonywać skoki na przemian po obu stronach minimum, co przypomina odbijanie się od ściany. W takich sytuacjach stosuje się mechanizmy wygładzające, takie jak momentum. Zmniejszają one ryzyko gwałtownych zmian kierunku.

Czy gradient descent pozostaje podstawą sztucznej inteligencji

Pomimo rozwoju coraz bardziej zaawansowanych technik optymalizacji, gradient descent wciąż pozostaje fundamentem uczenia modeli. Jego siła wynika z prostoty, elastyczności i możliwości stosowania w przestrzeniach o ogromnej liczbie parametrów. Niezależnie od tego, jak rośnie złożoność algorytmów, sedno procesu pozostaje takie samo: krok po kroku zmniejszać błąd, aż model znajdzie najbardziej trafne rozwiązanie.

Gradient descent to przykład tego, jak prosta idea może stać się jednym z filarów współczesnej technologii. Dzięki niemu modele uczą się patrzeć, słuchać i rozumieć. Każdy krok w dół po zboczu funkcji kosztu przybliża nas do inteligentnych narzędzi, które ułatwiają codzienność i rozszerzają granice możliwości AI.